Don Don - Drift detection method

MLOps란

MLops란 ML + Ops로 머신러닝 모형을 어떻게 운영하고 관리할 것인지에 대한 방법론
데이터 분석을 통해 서비스를 개선한다는 의미는 문제 정의 - 데이터 탐색 - 모형 개발 - 모형 배포 - 유지 관리 등의 일련의 절차들이 시스템화되는 것을 의미함
이 중 마지막 부분인 Monitoring 부분에 대해 알아보자

Monitoring

머신러닝 모형은 향후 데이터도 비슷한 데이터가 들어올 것이다를 가정함
- 주어진 데이터를 기준으로 모형을 구축하기 때문에 어쩔 수 없는 부분임
실제 모형을 구축하고 운영할 때 대부분의 경우 시간이 지날수록 모형의 성능은 떨어지는 경향이 있음
- drift가 발생한 경우(X의 분포가 바뀌었을 때, X와 Y의 관계가 바뀌었을 때 등)
모델을 production level에서 관리하기 위해서는 drift가 발생하는 경우를 지속적으로 모니터링해줘야 하며, 이상이 발생했을 시에 대응 시나리오가 존재해야 함
- X의 분포 변화 정도 or 모형 성능 변화에 따라 모델 retraining or rebuilding, .. etc

Drift란?

시간에 따른 데이터의 변화를 의미함
drift는 광의의 개념이고 Concept drift, Data drift, Label drift, Feature drift 등 다양한 종류의 drift가 존재함

concept drift

시간에 따른 X와 Y의 관계 변화를 의미함
- 고객이 구매한 제품을 예측할 때, 고객 선호도가 변경되는 경우
- 금융 위기 이후 회사의 수익을 예측하는 경우
X와 Y의 관계 변화는 하나로 정의할 수 없고, 다양한 시나리오가 있을 수 있음

full stack deeplearning lecture 11
- X와 Y의 분포 변화가 독립적으로 문제가 되는 것이 아니라 X의 분포가 바뀌면 Y의 분포도 바뀔 수 있고, $\hat{Y}$ 의 분포도 바뀔 수 있음 or 안바뀔 수도 있음

Drift 발생 시나리오 종류

instantaneous drift(shift)
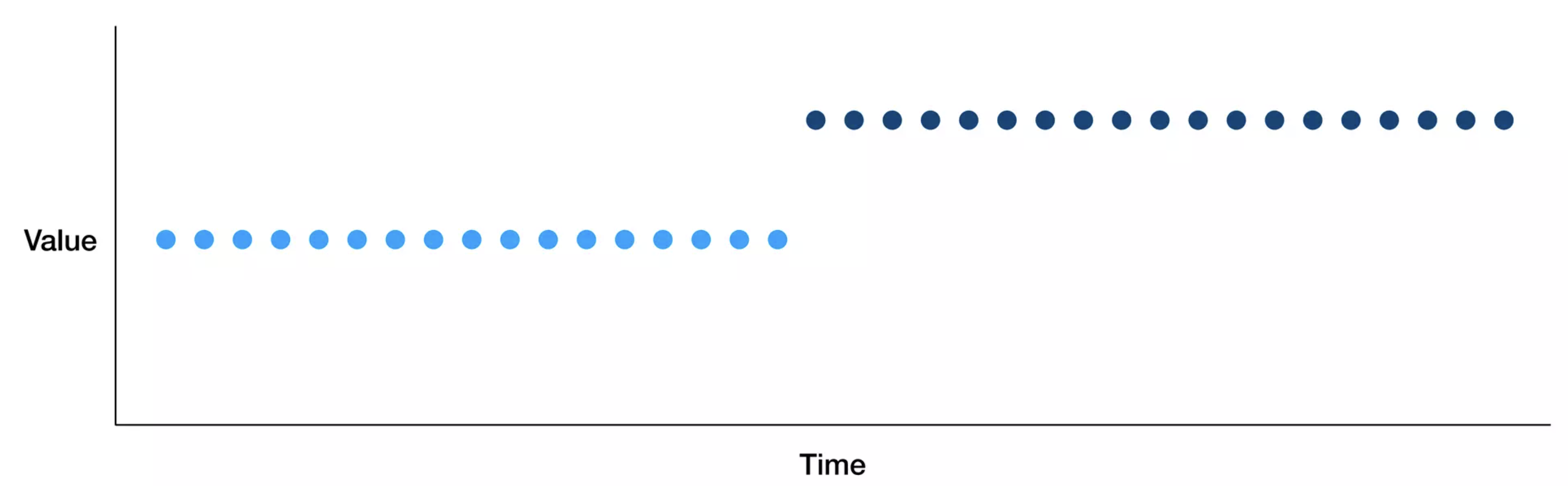
- 새로운 도메인에 기존 학습 모델을 배포하는 경우
- 전처리 파이프라인에서 버그가 발생하는 경우
- 외부 발생 요인(ex. covid)
Gradual drift
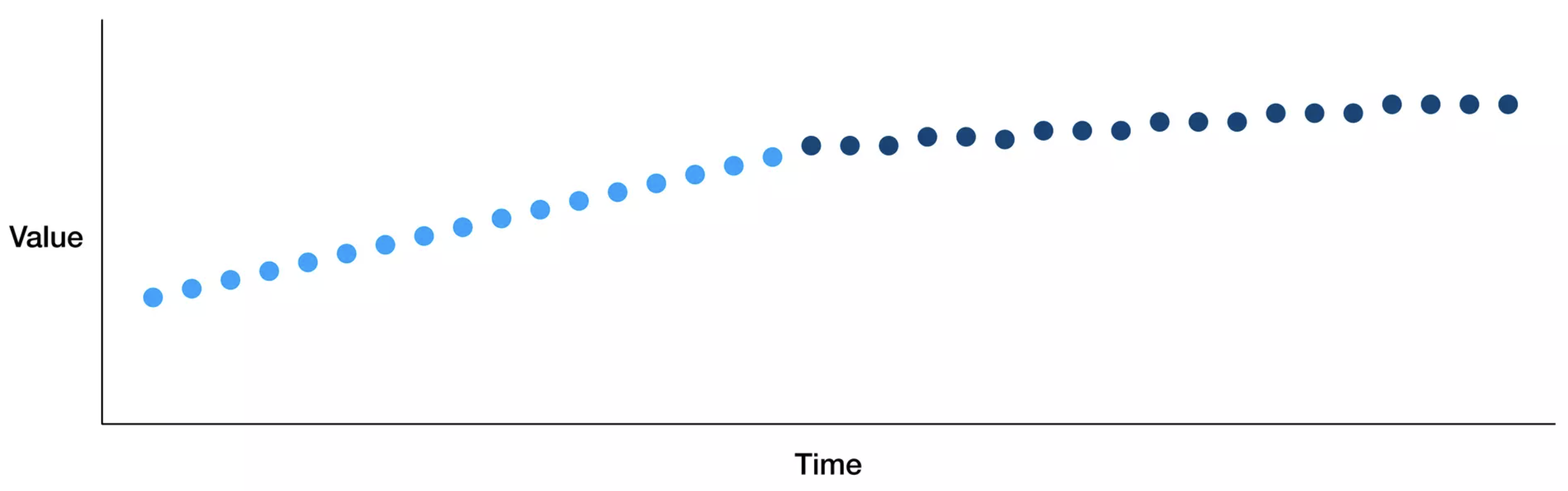
- 시간이 지나면서 유저 선호도가 바뀔 경우
- 시간이 지나면서 새로운 개념의 ex. 말뭉치가 도입되는 경우
Periodic drift
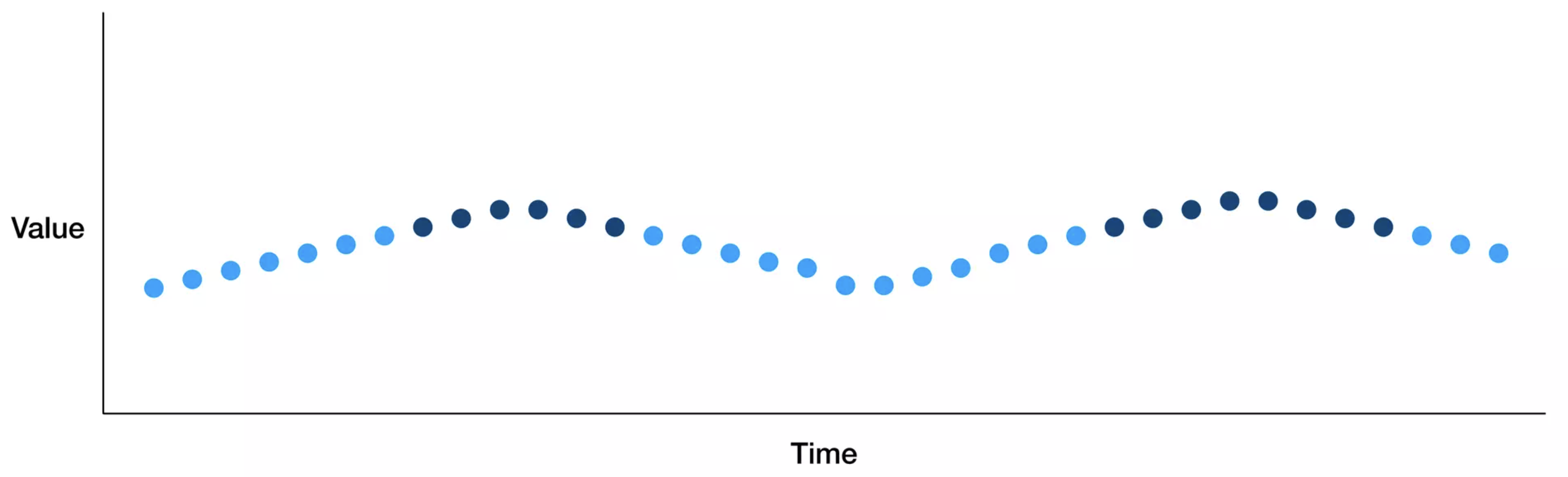
- 계절 요인이 존재할 경우
- 학습시 사용했던 시간대와 다른 시간대를 이용할 경우(ex. 오전 - 오후)
Temporary drift
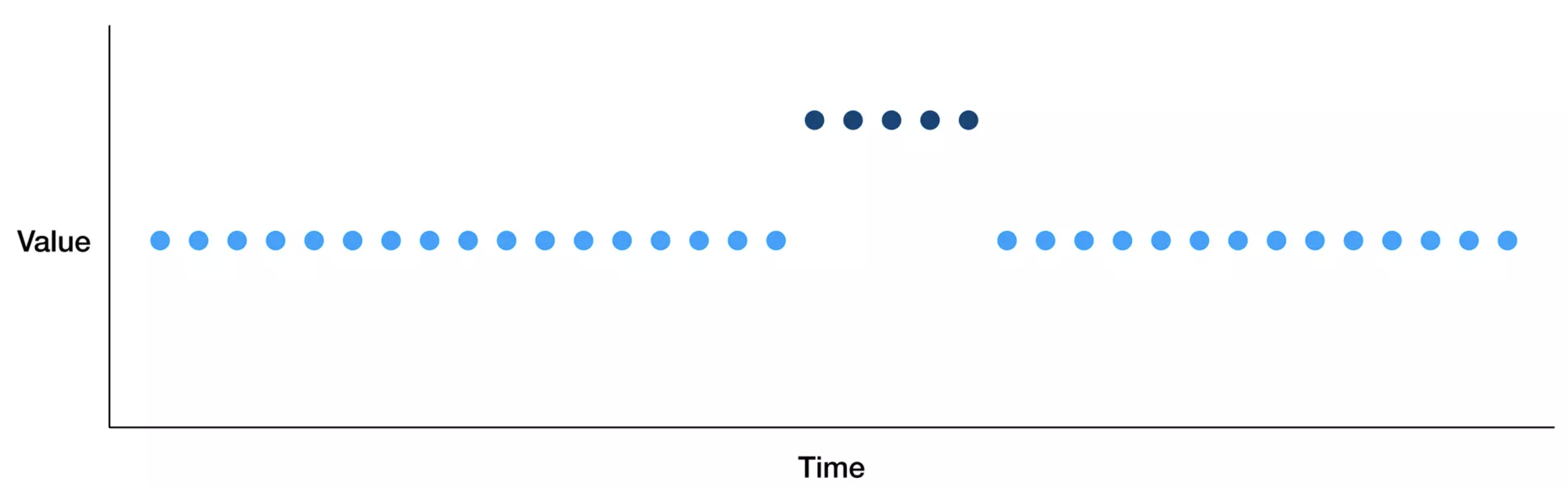
- 악의적인 유저가 모델을 공격하는 경우
- 인구통계학적으로 다르게 분류된 유저가 제품을 사용한 후 이탈한 경우

모니터링 방법

다양한 유형의 drift가 발생했을 때, 시나리오별로 대응 체계를 구축해야 함
핵심은 어떻게 drift를 판단할 수 있는지?
가장 간단하게는 target $Y$ 가 존재하는 경우 모델 성능의 변화를 보고 drift 여부를 탐지할 수 있음
또는 분포에 대한 통계 검정, 거리 측도 등을 통해 분포의 유사성을 판단할 수 있음
또는 Statistical process control을 통해 drift 발생 유무를 탐지할 수 있음

Divergence metrics

실제 모니터링 상황에서는 $Y$ 가 없는 경우가 빈번함
$Y$ 가 없을 때는 성능으로 drift를 탐지할 수 없고, 분포의 유사성을 측정하여 drift를 탐지해야 함
이 때 사용하는 것이 divergence metric임
Rule-based distance
- min, max, mean 등의 통계량을 비교
$f$ -divergence 기반
- KL-divergence
- Jensen-shannon divergence
- Hellinger divergence
- etc..

Example

import pandas as pd 
import numpy as np 

from sklearn.datasets import load_iris

# distance metrics 
from scipy.spatial.distance import jensenshannon
from scipy.special import rel_entr
from scipy.stats import chi2_contingency, ks_2samp, kstwo, wasserstein_distance

Example data

data = load_iris()
iris_data = pd.DataFrame(np.c_[data.data, data.target], columns=data.feature_names + ['target'])
iris_two = iris_data[iris_data.target!= 2]
iris0 = iris_two[iris_two.target==0]

# Divide the data into two set _1 and _2
iris0_1 = iris0.iloc[:25]
iris0_2 = iris0.iloc[25:]


data = iris0_2.iloc[:, 0]
reference_data = iris0_1.iloc[:, 0]

Histogram 생성

분포 생성 방법은 가장 간단하게는 histogram부터 kernel density 등 다양한 방법이 있음
이 중 히스토그램을 이용해서 분포를 생성함
- 히스토그램에서 bin을 나누는 방식도 다양한 방법이 있음
  - “scott”, “sturges”, “fd”, “doane”, .. etc
- 이 중 non-normal data에 비교적 성능이 좋은 “donna” 방법 이용
  - drift 탐지 관련 패키지인 nannyml에서도 이 방법을 이용함

$n_{h} = 1 + \log_{2} (n) + \log_{2} (1 + \frac{| g_{1} |}{σ_{g_{1}}}) g_{1} = m e a n [{(\frac{x - μ}{σ})}^{3}] σ_{g_{1}} = \sqrt{\frac{6 (n - 2)}{(n + 1) (n + 3)}}$

def make_hist(reference_data, data):
    len_reference = len(reference_data)
    bins = np.histogram_bin_edges(reference_data, bins='doane')
    reference_proba_in_bins = np.histogram(reference_data, bins=bins)[0] / len_reference 

    len_data = len(data)
    data_proba_in_bins = np.histogram(data, bins=bins)[0] / len_data # reference data 기준 bins 

    leftover = 1 - np.sum(data_proba_in_bins) 
    if leftover > 0:
        data_proba_in_bins = np.append(data_proba_in_bins, leftover)
        reference_proba_in_bins = np.append(reference_proba_in_bins, 0)

    return reference_proba_in_bins, data_proba_in_bins

$f$ divergence

$D_{f} (P | | Q) = \sum q (x) \cdot f (\frac{p (x)}{q (x)})$

KL-divergence

$K L (P | | Q) = \sum p (x) \cdot l o g (\frac{p (x)}{q (x)})$

def kl_divergence(reference_data, data):
    """
    참고 : https://github.com/NannyML/nannyml/blob/3c6504660f2fb301e549bdf80ca56c4b114fba06/nannyml/drift/univariate/methods.py#L260
    from scipy.special import rel_entr
    """  
    
    P, Q = make_hist(reference_data, data)
    
    epsion = 0.000001
    P = P + epsion
    Q = Q + epsion

    vec = rel_entr(P, Q)
    distance = np.sum(vec)
    return distance

kl_divergence(reference_data, data)

1.5021860165248588

정규분포일 때, KL-divergence

\begin{aligned} \int [\log (p (x)) - \log (q (x))] p (x) d x & = \int [- \frac{1}{2} \log (2 π) - \log (σ_{1}) - \frac{1}{2} {(\frac{x - μ_{1}}{σ_{1}})}^{2} + \frac{1}{2} \log (2 π) + \log (σ_{2}) + \frac{1}{2} {(\frac{x - μ_{2}}{σ_{2}})}^{2}] \times \frac{1}{\sqrt{2 π} σ_{1}} \exp [- \frac{1}{2} {(\frac{x - μ_{1}}{σ_{1}})}^{2}] d x \\ = \int {\log (\frac{σ_{2}}{σ_{1}}) + \frac{1}{2} [{(\frac{x - μ_{2}}{σ_{2}})}^{2} - {(\frac{x - μ_{1}}{σ_{1}})}^{2}]} \times \frac{1}{\sqrt{2 π} σ_{1}} \exp [- \frac{1}{2} {(\frac{x - μ_{1}}{σ_{1}})}^{2}] d x \\ = E_{1} {\log (\frac{σ_{2}}{σ_{1}}) + \frac{1}{2} [{(\frac{x - μ_{2}}{σ_{2}})}^{2} - {(\frac{x - μ_{1}}{σ_{1}})}^{2}]} \\ = \log (\frac{σ_{2}}{σ_{1}}) + \frac{1}{2 σ_{2}^{2}} E_{1} {(X - μ_{2})^{2}} - \frac{1}{2 σ_{1}^{2}} E_{1} {(X - μ_{1})^{2}} \\ = \log (\frac{σ_{2}}{σ_{1}}) + \frac{1}{2 σ_{2}^{2}} E_{1} {(X - μ_{2})^{2}} - \frac{1}{2} \\ = \log (\frac{σ_{2}}{σ_{1}}) + \frac{1}{2 σ_{2}^{2}} [E_{1} {(X - μ_{1})^{2}} + 2 (μ_{1} - μ_{2}) E_{1} {X - μ_{1}} + (μ_{1} - μ_{2})^{2}] - \frac{1}{2} \\ = \log (\frac{σ_{2}}{σ_{1}}) + \frac{σ_{1}^{2} + (μ_{1} - μ_{2})^{2}}{2 σ_{2}^{2}} - \frac{1}{2} . \end{aligned}

def gaussian_kl_divergence(reference_data, data): 
    
    epsion = 0.000001
    P = reference_data + epsion
    Q = data + epsion

    mu1 = np.mean(P)
    mu2 = np.mean(Q)

    sig1 = np.std(P)
    sig2 = np.std(Q)

    mu_diff = pow(mu1 - mu2, 2)
    sig_diff = sig1**2 - sig2**2

    distance = np.log(sig2/sig1) + (mu_diff + sig_diff)/(2*sig2**2)
    return distance

gaussian_kl_divergence(reference_data, data)

0.10386846525275067

Exponential divergence

$E x = \sum p (x) \cdot l o g^{2} (\frac{p (x)}{q (x)})$

def exponential_divergence(reference_data, data):
   
    P, Q = make_hist(reference_data, data)
    
    epsion = 0.000001
    P = P + epsion
    Q = Q + epsion

    distance = np.sum(P*(np.log(P/Q))**2)
    return distance


exponential_divergence(reference_data, data)

16.544668384201483

Pearson divergence

$p r = \sum q (x) \cdot (\frac{p (x)}{q (x)} - 1)^{2}$

def pearson_divergence(reference_data, data):
   
    P, Q = make_hist(reference_data, data)
    
    epsion = 0.000001
    P = P + epsion
    Q = Q + epsion

    distance = np.sum(Q*(((P/Q)-1)**2))
    return distance


pearson_divergence(reference_data, data)

14400.29444211036

Squared hellinger divergence

$S h = \sum q (x) \cdot (\sqrt{\frac{p (x)}{q (x)}} - 1)^{2}$

def hellingar_distance(reference_data, data):
    """
    참고 : https://github.com/NannyML/nannyml/blob/3c6504660f2fb301e549bdf80ca56c4b114fba06/nannyml/drift/univariate/methods.py#L260
    distance = np.sqrt(np.sum((np.sqrt(P) - np.sqrt(Q)) ** 2)) / np.sqrt(2)
    """
    P, Q = make_hist(reference_data, data)
    
    epsion = 0.000001
    P = P + epsion
    Q = Q + epsion

    distance = np.sum(Q*((np.sqrt(P/Q)-1)**2))
    return distance


hellingar_distance(reference_data, data)

0.30639829306375294

Jeffrey divergence

$J e f = \sum (p (x) - q (x)) \cdot l o g \frac{p (x)}{q (x)}$

def jeffrey_distance(reference_data, data):

    P, Q = make_hist(reference_data, data)
    
    epsion = 0.000001
    P = P + epsion
    Q = Q + epsion

    distance = np.sum((P - Q)*np.log(P/Q))
    return distance

jeffrey_distance(reference_data, data)

3.4329079921766494

Renyi divergence

$R i = \frac{1}{α - 1} \cdot l o g (\sum \frac{p (x)^{α}}{q (x)^{α - 1}}), 0 < α < i n f$

renyi divergence는 kl divergence의 일반화 꼴
$α = 1$ 일 때 Kl-divergence

def renyi_distance(reference_data, data, alpha):

    """
    참고 : https://en.wikipedia.org/wiki/R%C3%A9nyi_entropy
    """

    P, Q = make_hist(reference_data, data)
    
    epsion = 0.000001
    P = P + epsion
    Q = Q + epsion

    if alpha < 0: 
        raise ValueError("'number' must be positive")
    
    if alpha == 1: 
        raise ValueError("'number' cannot be 1")

    distance = 1/(alpha -1)*np.sum(np.log(P**alpha) - np.log(Q**(alpha-1)))
    return distance

renyi_distance(reference_data, data, alpha = 0.01)

25.52115244332236

Chernoff divergence

$C h = - l o g (\sum \frac{p (x)^{α}}{q (x)^{α - 1}}), 0 \leq α \leq 1$

def chernoff_distance(reference_data, data, alpha):
     
    """
    https://threeplusone.com/pubs/on_information.pdf
    """

    P, Q = make_hist(reference_data, data)
    
    epsion = 0.000001
    P = P + epsion
    Q = Q + epsion

    if alpha < 0: 
        raise ValueError("'number' must be positive")
    
    if alpha > 1: 
        raise ValueError("'number' must be less than 1")
    
    #distance = 4/(1 - alpha**2)*np.sum(Q*(1 - (Q/P)^((1+alpha)/2)))
    distance = -np.log(np.sum((P**alpha)/(Q**(alpha-1))) )
    return distance

chernoff_distance(reference_data, data, alpha = 0.01)

0.018358570378002852

Alpha-Beta divergence

$A B = - \frac{1}{α β} \cdot \sum (p (x)^{α} q (x)^{β} - \frac{α}{α + β} p (x)^{α + β} - \frac{β}{α + β} q (x)^{α + β})$

def alpha_beta_distance(reference_data, data, alpha, beta):
    
    """
    https://arxiv.org/pdf/1805.01045.pdf
    """
    
    P, Q = make_hist(reference_data, data)
    
    epsion = 0.000001
    P = P + epsion
    Q = Q + epsion
    
    distance = (-1/(alpha*beta))*np.sum((P**alpha*Q**beta) - (alpha/(alpha + beta))*(P**(alpha + beta)) - (beta/(alpha + beta))*(Q**(alpha + beta)))
    return distance

alpha_beta_distance(reference_data, data, alpha = 0.01, beta = 0.02)

111.42684257864133

Jensen shannon divergence

def js_divergence(reference_data, data):

    P, Q = make_hist(reference_data, data)
    
    epsion = 0.000001
    P = P + epsion
    Q = Q + epsion

    distance = jensenshannon(P, Q, base=2)
    return distance

js_divergence(reference_data, data)

0.3999777589033326

Total variance divergence

$T v = \frac{1}{2} \cdot \sum | p (x) - q (x) |$

def total_variation_distance(reference_data, data):

    P, Q = make_hist(reference_data, data)
    
    epsion = 0.000001
    P = P + epsion
    Q = Q + epsion

    distance = 0.5 * np.sum(np.abs(P - Q))
    return distance

total_variation_distance(reference_data, data)

0.27999999999999997

Statistical process control

새로 들어온 데이터에 대해 사전에 정의한 오류율과 기준으로 drift를 감지하는 방법
- Drift detection method(DDM)
  - 각 데이터 샘플에 대한 예측 오류를 베르누이 확률변수로 나타내고, n 개 중에 발생한 오류의 수의 비율을 나타내는 오류율의 평균에 대한 신뢰구간 추정을 통해 오류율이 급격하게 증가하는 부분을 탐지
  - warning level : $p_{t} + s_{t} \geq p_{m i n} + 2 \cdot s_{m i n}, p_{t} : prob of misclassification, s_{i} : std$
  - change level : $p_{t} + s_{t} \geq p_{m i n} + 3 \cdot s_{m i n}$
  - 오류율이 천천히 변화할 경우 감지 성능이 떨어짐
- Early drift detection method(EDDM)
  - DDM에서 정의한 오류 횟수 대신에 두 오류 사이의 거리를 이용하여 gradual drift에 대한 탐지
  - warning level : $\frac{(p_{t} + 2 \cdot s_{t})}{(p_{m a x} + 2 \cdot s_{m a x})} < α = 0.9$
  - EDDM은 gradual drift에 대한 변화 탐지에 주로 활용됨
- CUMSUM test
  - input data $x_{1}, \dots, x_{t}$
    
    $\begin{aligned} g_{0} & = 0 \\ g_{t} & = m a x (0, g_{t - 1} + (x_{t} - v)), v : parameter(given) \end{aligned}$
  - $g_{t} > λ$ 일 경우 change point로 탐지, $g_{t} = 0$ 으로 초기화( $λ$ : threshold(given))
    - $v, λ$ 에 따라 성능이 유동적임
- page-hinkley test : CUMSUM test에서 파생된 test
  - $m_{T} = \sum_{t = 1}^{T} (x_{t} - {\bar{x}}_{T} - δ), {\bar{x}}_{T} = \frac{1}{T} \sum_{t = 1}^{t} x_{t}, δ : 허용되는 변화의 크기(given)$
  - $M_{T} = m i n (m_{t}, t = 1, \dots, T)$
  - test monitors : $P H_{T} = m_{T} - M_{T} > λ, λ : threshold(given)$
    - $λ$ 를 작게 설정할 경우 거의 모든 change point를 감지할 수 있지만, 잘못 감지할 확률이 증가
  - 이전 데이터와 새로 들어온 데이터 간에 연관성이 작을 수 있음
  - $m_{t}$ 를 정의할 때 fading factor를 도입함
    - $m_{T} = f a d i n g F a c t o r \times m_{T} + (x_{t} - {\bar{x}}_{T} - δ), f a d i n g F a c t o r : [0, 1] (parameter(given)$

Time data based method

ADWIN : window 내에 두 개의 subwindow를 비교하면서 두 개의 subwindow가 사전에 정한 $ϵ_{c}$ 만큼 충분히 다르다면 concept drift가 존재한다고 판단하는 알고리즘

book : Anomaly detection through stream processing, Knowledge Discovery from Data Streams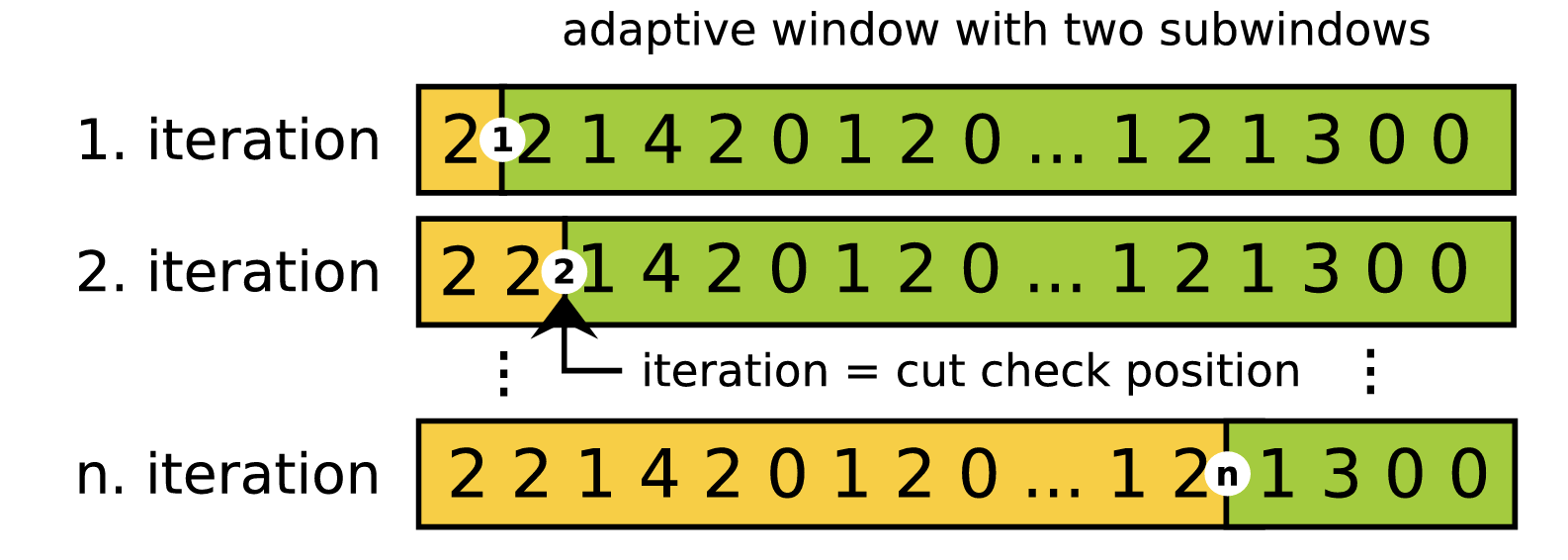
- $m = \frac{2}{\frac{1}{| W_{0} |} + \frac{1}{| W_{1} |}}$
- $ϵ_{c u t} = \sqrt{\frac{1}{2 m} \cdot l n \frac{4 | W |}{δ}}$
paper : Scalable Detection of Concept Drifts on Data Streams with Parallel Adaptive Windowing

그림을 통해 보면 정해진 window $W$ 에서 두 개의 subwindow를 나눈다. 각 subwindow에서 ${\hat{μ}}_{W_{0}}$ 와 ${\hat{μ}}_{W_{1}}$ 을 계산한다. subwindow를 한 칸씩 sliding해나가면서 $| {\hat{μ}}_{W_{0}} - {\hat{μ}}_{W_{1}} | \geq ϵ_{c}$ 조건을 만족할 때까지 반복한다. 조건을 만족할 경우 $W$ 의 head 값(old data)을 삭제한다. 문제는 subwindow를 조합별로 계산해야 하므로 계산 효율성이 매우 떨어진다.

참고 자료

MLops 관련

page-Hinkley and ADWIN

책 : Anomaly detection through stream processing, Knowledge Discovery from Data Streams
https://github.com/blablahaha/concept-drift/blob/master/concept_drift/page_hinkley.py
https://www.facom.ufu.br/\~elaine/disc/MFCD2018/

Citation

BibTeX citation:

@online{don2024,
  author = {Don, Don and Don, Don},
  title = {Drift Detection Method},
  date = {2024-03-09},
  url = {https://dondonkim.netlify.app/posts/2022-03-01-distance/distance.html},
  langid = {en}
}

For attribution, please cite this work as:

Don, Don, and Don Don. 2024. “Drift Detection Method.” March 9, 2024. https://dondonkim.netlify.app/posts/2022-03-01-distance/distance.html.