Don Don - partial R squared

library(tidyverse)
library(easystats)
library(GGally)
library(skimr)
library(broom)
library(ggdag)
library(dagitty)
library(broom)

#data("msleep")

partial $R^{2}$

먼저 $R^{2}$ 는 $Y$ 의 총 분산 중 $X$ 에 의해 설명되는 분산의 비율을 의미합니다(오른쪽 그림 참고).

partial $R^{2}$ 는 “partial”의 의미 그대로 다른 변수들의 관계를 제거하고 $Y$ 의 변동에 기여하는 순수한 $X$ 의 변동을 의미합니다. partial $R^{2}$ 는 sensitivity analysis에 이용할 수 있습니다.

set.seed(1)
dagify(Y ~ X1,
       X1 ~ eX1,
       eX1 ~~ eY, 
       Y ~ eY,
       Y ~ X2,
       X1 ~ X2) %>% 
  ggdag() + 
    theme_minimal()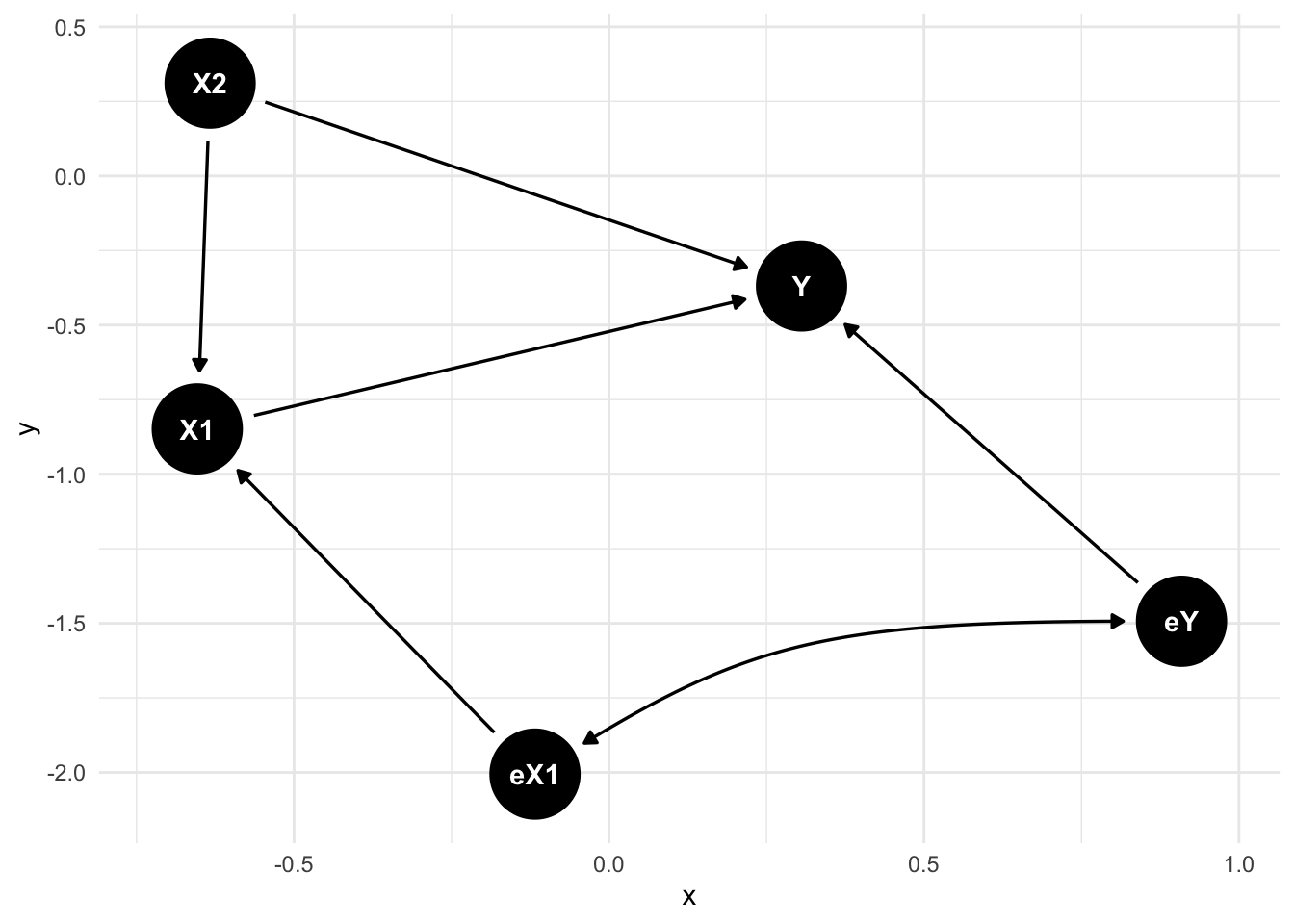

그림을 통해 보면 X2는 confounder로 X1과 Y에 동시에 영향을 주는 변수입니다. 이 때, confounder의 효과를 제거하고 Y ~ X1의 효과를 보려고 합니다. 이 경우 partial $R^{2}$ 를 이용할 수 있습니다.

partial $R^{2}$ 는 Y의 변동 중 confounder X2을 통제했을 때, X1가 설명하는 변동의 비율을 의미합니다.

$R_{Y \sim X_{1} | X_{2}}^{2} = \frac{S S E (X_{2}) - S S E (X_{1}, X_{2})}{S S E (X_{2})}$

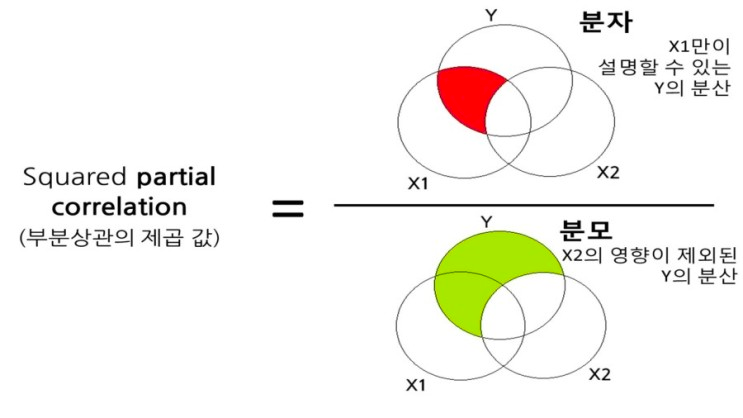
Example

data description

포유류의 수면과 관련된 데이터

sleep_total : 총 수면 시간 ( $Y$ )
brainwt : 뇌의 무게
bodywt : 체중

brainwt( $X_{1}$ )의 partial $R^{2}$ 를 계산해보겠습니다.

dat <- read_csv("./msleep.csv")

corr <- dat %>% 
    cor()
corr

            sleep_total    brainwt     bodywt
sleep_total   1.0000000 -0.6806058 -0.6810127
brainwt      -0.6806058  1.0000000  0.9448724
bodywt       -0.6810127  0.9448724  1.0000000

먼저 correlation(zero-order-correlation)를 보면 sleep_total과 brainwt의 correlation는 $- 0.68$ 로 강한 음의 상관관계가 존재하는 것을 볼 수 있습니다. correlation 패키지에 partial correlation을 계산하는 함수가 이미 있으므로 이용해보겠습니다.

cor_to_pcor(corr)

            sleep_total    brainwt     bodywt
sleep_total   1.0000000 -0.1548778 -0.1580967
brainwt      -0.1548778  1.0000000  0.8972459
bodywt       -0.1580967  0.8972459  1.0000000

sleep_total과 brainwt의 partial correlation는 $- 0.15$ 로 이전 zero-order-correlation과 달리 약한 음의 상관관계가 존재하는 것을 볼 수 있습니다.

cor_to_pcor(corr)^2

            sleep_total    brainwt     bodywt
sleep_total  1.00000000 0.02398713 0.02499458
brainwt      0.02398713 1.00000000 0.80505014
bodywt       0.02499458 0.80505014 1.00000000

partial $R^{2}$ 를 구해보면 $0.023$ 정도인 것을 볼 수 있습니다. 변수의 의미를 보면 brainwt( $X_{1}$ )는 bodywt( $X_{2}$ )의 일부입니다. 따라서 bodywt( $X_{2}$ )를 통제했을 때, brainwt( $X_{1}$ )가 설명하는 $Y$ 의 변동은 미미하다고 볼 수 있습니다.

ANOVA table을 이용해서 다시 계산해보겠습니다.

fit_f <- lm(sleep_total ~ ., dat)
fit_b <- lm(sleep_total ~ bodywt, dat)
fit_f_anov <- anova(fit_f) %>% tidy()
fit_b_anov <- anova(fit_b) %>% tidy()

(fit_b_anov$sumsq[2] - fit_f_anov$sumsq[3])/fit_b_anov$sumsq[2]

[1] 0.02398713

결과는 동일한 것을 확인할 수 있습니다.

fit1 <- lm(sleep_total ~ bodywt, dat)
fit2 <- lm(brainwt ~ bodywt, dat)

r1 <- augment(fit1)$.resid
r2 <- augment(fit2)$.resid

cor(r1, r2)^2

[1] 0.02398713

semi partial(or part) $R^{2}$

set.seed(12)
dagify(X1 ~ X2, 
       X1 ~ eX1, 
       Y ~ X1, 
       Y ~ eX1) %>% 
  ggdag() + 
    theme_minimal()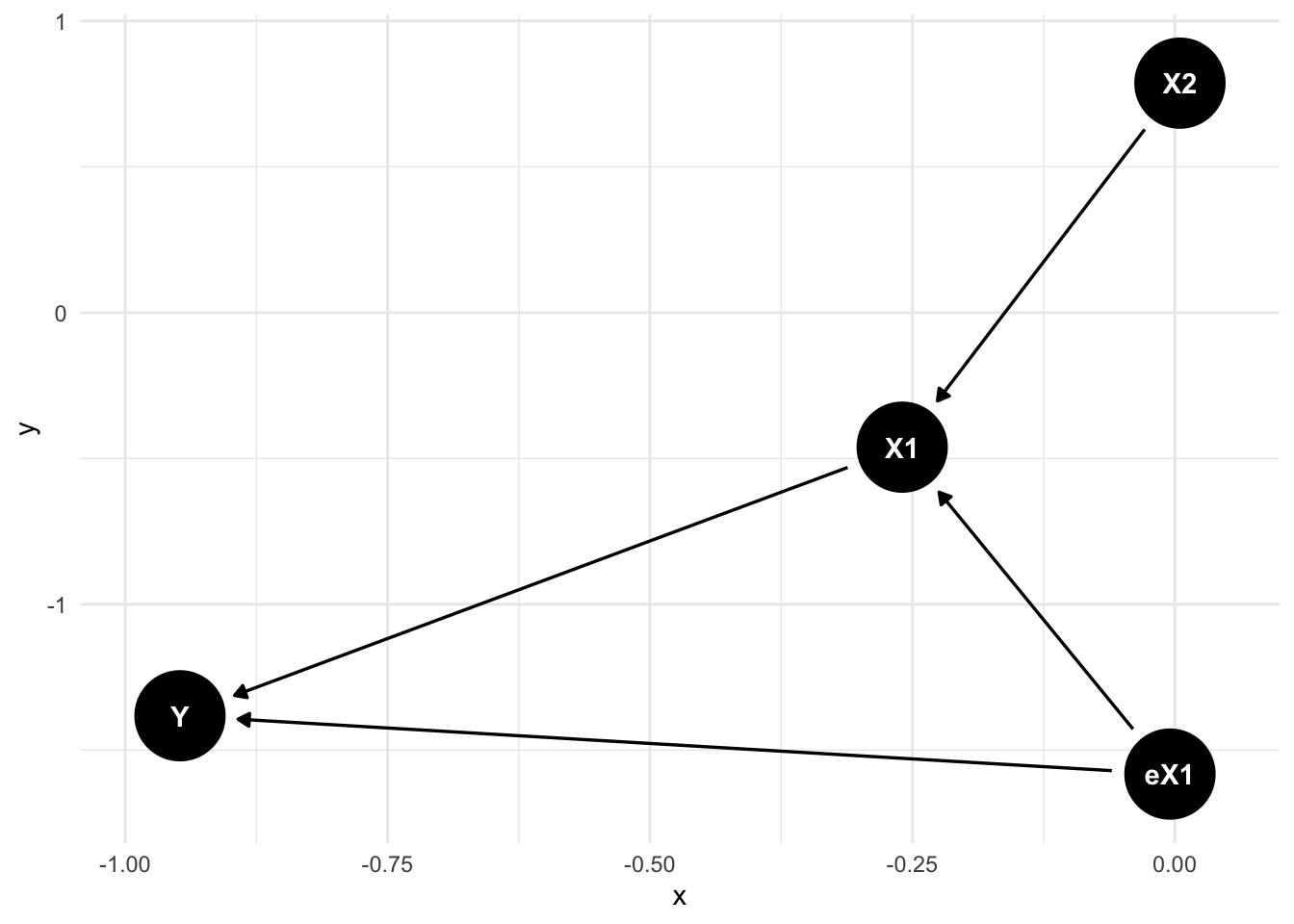

semi partial(or part) $R^{2}$ 는 Y의 변동 중 변수를 추가했을 때, 추가한 변수가 설명하는 변동의 비율을 의미합이다. semi partial(or part) $R^{2}$ 와 partial $R^{2}$ 의 차이는 confounder가 Y와 $X$ 에 동시에 영향을 미치는지, 혹은 $X$ 에만 영향을 미치는지로 볼 수 있습니다.

$s r_{1}^{2} = r_{y, (1.2)}^{2} = (\frac{r_{y .1} - r_{y .2} \cdot r_{1.2}}{\sqrt{1 - r_{1.2}^{2}}})^{2}$

$s r_{1}^{2} = R_{y, 1.2}^{2} - r_{y .2}^{2}$

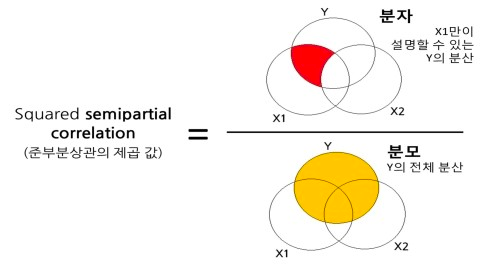
Example

sleep_total( $Y$ )의 분산 중 brainwt( $X_{1}$ )가 설명하는 순수 비율을 계산하려고 합니다. (bodywt( $X_{2}$ ) 제외)

cor_to_spcor(corr, cov = sapply(dat, sd))

            sleep_total    brainwt     bodywt
sleep_total  1.00000000 -0.1134126 -0.1158295
brainwt     -0.05071300  1.0000000  0.6573670
bodywt      -0.05176701  0.6570276  1.0000000

semi-partial correlation을 구해보면 partial correlation과 비슷하게 $s r_{1}^{2} = - 0.11$ 로 correlation과 큰 차이가 있는 것을 볼 수 있습니다.

cor_to_spcor(corr, cov = sapply(dat, sd))^2

            sleep_total    brainwt     bodywt
sleep_total 1.000000000 0.01286242 0.01341648
brainwt     0.002571808 1.00000000 0.43213138
bodywt      0.002679823 0.43168533 1.00000000

semi-partial $R^{2}$ 를 구해보면 $0.012$ 입니다. 이전과 마찬가지로 변수의 의미를 보면 brainwt( $X_{1}$ )는 bodywt( $X_{2}$ )값의 일부입니다. 따라서 brainwt( $X_{1}$ )가 설명하는 $Y$ 의 변동은 미미하다고 볼 수 있습니다.

fit1 <- lm(sleep_total ~ bodywt + brainwt, dat)
fit2 <- lm(sleep_total ~ bodywt, dat)

r2_y12 <- broom::glance(fit1)$r.squared
r2_y2 <- broom::glance(fit2)$r.squared

r2_y12 - r2_y2

[1] 0.01286242

이는 단순하게 full model의 $R^{2}$ 에서 $Y \sim X_{1}$ 의 $R^{2}$ 의 차이를 통해서도 구할 수 있다( $R_{y, 1.2}^{2} - r_{y .2}^{2} = 0.4766408 - r 2_{y} 2$ )

fit3 <- lm(brainwt ~ bodywt, dat)

cor(augment(fit3)$.resid, dat$sleep_total)^2

[1] 0.01286242

또는 $X_{1} \sim X_{2}$ 의 잔차( $X_{1}$ 에서 $X_{2}$ 가 설명하는 부분을 제외한 부분)와 $Y$ 와의 상관계수의 제곱을 통해서도 마찬가지로 구할 수 있다.

참고자료

http://campus.murraystate.edu/academic/faculty/cmecklin/STA565/_book/correlations-multiple-and-partial.html

https://brendanhcullen.github.io/psy612/lectures/7-partial.html#25

https://rpubs.com/KwonPublishing/249631

https://easystats.github.io/correlation/reference/cor_to_pcor.html

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=soowon0109&logNo=30173631827

Citation

BibTeX citation:

@online{don2022,
  author = {Don, Don and Don, Don},
  title = {Partial {R} Squared},
  date = {2022-08-31},
  url = {https://dondonkim.netlify.app/posts/2022-08-31-partial-correlation/partial_corr.html},
  langid = {en}
}

For attribution, please cite this work as:

Don, Don, and Don Don. 2022. “Partial R Squared.” August 31, 2022. https://dondonkim.netlify.app/posts/2022-08-31-partial-correlation/partial_corr.html.

partial R2

Example

semi partial(or part) R2

Example

참고자료

Citation

partial $R^{2}$

semi partial(or part) $R^{2}$